Multiplicative Weights

Multiplicative weights update algorithm

This is one of many classical optimization techniques.

People tend not to learn it as an undergrad for two reasons.

1. The proofs that it has good properties are fairly unintuitive, and require fairly significant mathematical sophistication
2. The most important problems it tries to solve require substantial backgrounds to even understand why the problems are important

There are many good papers out there that describe multiplicative weights mathematically, such as this one: good multiplicative weights article (not mine)

However, this does not do a great job at communicating why it works, and certainly it is difficult to see how people would have came up with it.

But the truth is that this is not a difficult algorithm to invent. Many different people from many fields of study independently invented this method to solve the problem at hand. So I hope to show how one might invent a method like this, in the hopes that it communicates how it works better than other explanations. In order to do that, we really have to look at the dynamics of specific optimization problems.

Online case

Weighted majority

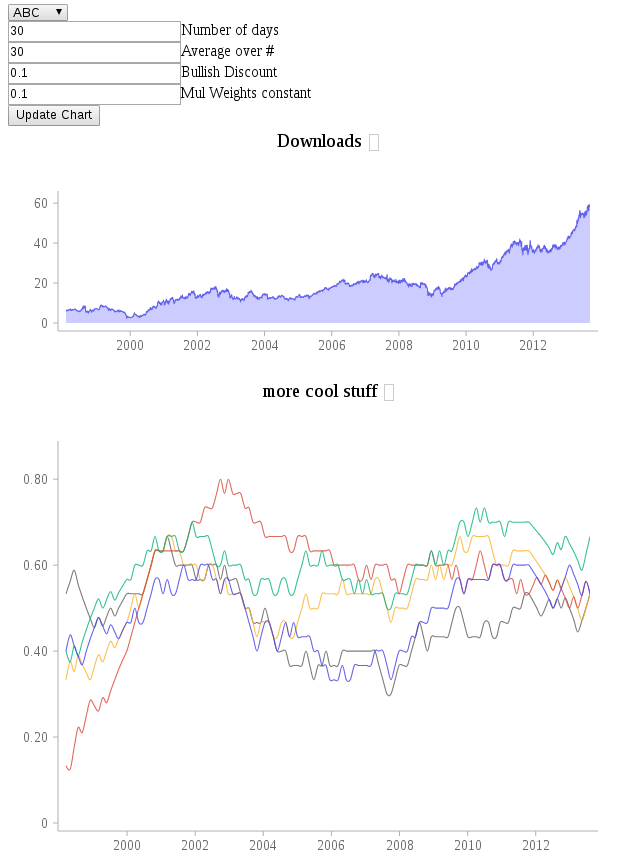
Stock market weighted average case

The idea is that you can create a whole bunch of generic strategies, and combine them using multiplicative weights.

Core strategies are:

• Optimistic: Always increasing
• Skittish: if it decreases, it will decrease again, increases, increase again
• Bullish: Long term trajectory is indicator
• Chaotic: Uniformly random
• negation of all these strategies (i.e. the pessimistic strategy that always decreases, the reverse skittish strategy, trend-breaking strategy, etc)

Note about strategies.

These strategies are not chosen randomly. Each one has nice properties. Uniform random allows us to model chaotic events. Optimism takes care of standard trend of stocks over time. Bullish takes into account long term behavior. Skittish takes into account short term behavior. Negated strategies allow for reversals. All in all, you should be able to describe just about any decent strategy as a simple combination of these. Which is exactly what we are trying to do.

Algorithm

1. Take each strategy as an advisor.
2. etc.

On real data:

Offline case

Zero sum games (simultaneous tick tack toe)

Ruleset

• Players choose next location independently only valid locations are empty ones
• If both players choose same location at the time step, then it is taken by a special token indicating that both and X and an O is there for scoring
• If the game ends with a 3 in a row of both Xs and Os, then there is a tie

Example game:

X | _ | _
_ | O | _
_ | _ | _

Both players choose lower right, so it is a Q

X | _ | _
_ | O | _
_ | _ | Q


X | _ | X
_ | O | _
O | _ | Q


X | O | X
_ | O | X
O | _ | Q

X wins

So one question is: What is the optimal strategy? Unlike regular tick tack toe, the optimal strategy requires a probability distribution of different choices.

Demonstration:

_ | _ | X
X | O | _
O | _ | _

If you look carefully, there is no single optimal choice for either X or O. O can force a tie by playing lower center coordinate (1,2) or (2,2). But O has the upper hand, so it seems like it can do better. Especially because it does not look like X can force a tie this move. But on the other hand, any particular move O makes can be easily countered by X. So in other words, O has to move probabilistically in order to have a strategy that has an expected value better than a tie. And X has to have a probabilistic strategy that best counters O’s probabilistic strategy.

So how do we actually build an perfect AI for this game?

In regular tick tack toe, we can create an optimal strategy by enumerating all \(9^3=729\) game states, and working backwards.

This will not work here because some of the optimal strategies are probabilistic, due to this simultaneous movement.