Understanding the mechanics of deep learning
Understanding the mechanics of deep learning
Problems deep learning tries to solve
Image Analysis: Text reading
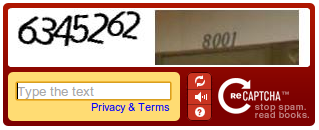
Consider the CAPTCHA problem:
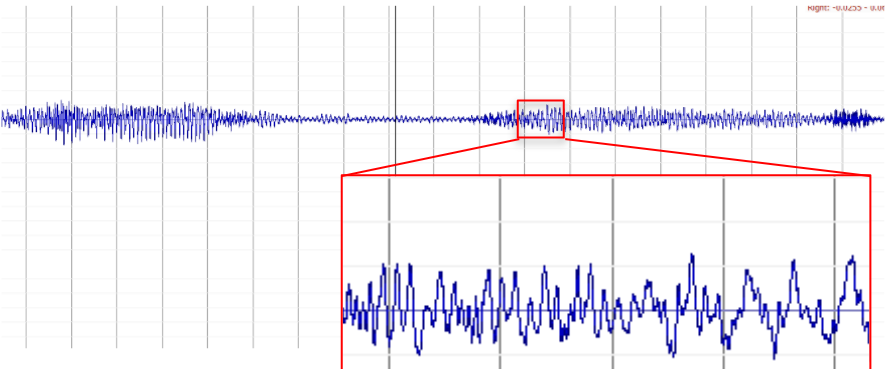
Speech recognition
To see why speech is so hard, just look at it:
This is the visual representation of this:
Now, if you know about sound, then you know that a lot of this information is really just overlapping frequencies and volumes which can be extracted and turned into a form which is easier to work with.
Unfortunately, humans can understand sounds with differnet
- Pitch/Frequency
- Volume/Amplitude
- Speed of changes (talking faster)
- Distorters
Not only that, but we humans are able to understand many different languages by learning them. So we already know that any model of reasonable complexity will work anyways.
Requirements to solve these problems
- Learning
- Filtering out noise
- Abstracting shapes
- Compressing data
Key ideas of deep learning, and how they try to solve those problems
Gradient descent
NN function (activation/mat mul)
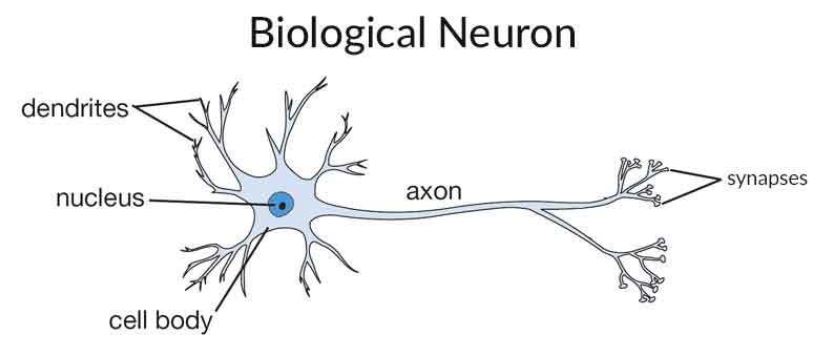
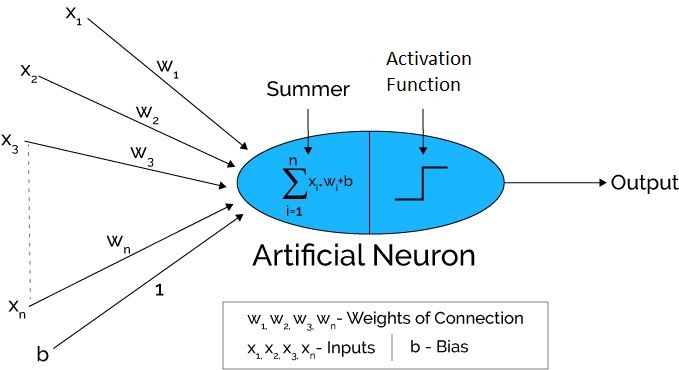 \(y = \sigma(\bar{a} \cdot \bar{x} + b)\)
\(y = \sigma(\bar{a} \cdot \bar{x} + b)\)
Stacking and Layering
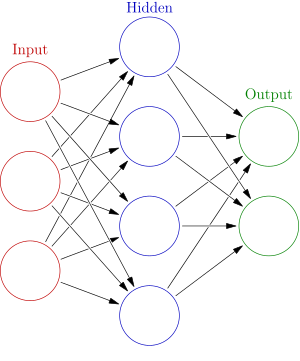
\(\text{hidden} = \sigma(W_1 \cdot \text{input} + b_1)\) \(\text{output} = \sigma(W_2 \cdot \text{hidden} + b_2)\)
Backpropagation
Learning representations by back-propagating errors
Bad example of backpropagation explanation
A slightly better backpropagation explanation
Yet another backpropagation algorithm
Formulas
\[\text{lin-hidden}_i = \sum_j W^1_{ij} \cdot \text{input}_j + b^1_i\] \[\text{hidden}_i = \sigma\left(\text{linhidden}_i \right)\] \[\text{lin-out}_i = \sum_j W^2_{ij} \cdot \text{hidden}_j + b^2_i\] \[\text{output}_i = \sigma\left( \text{lin-out}_i \right)\] \[\text{cost} = \sum_i (\text{output}_i - \text{actual}_i)^2\] \[\text{outerr}_i = (\text{output}_i - \text{actual}_i)\] \[\text{hiderr}_i = \sigma^\prime\left(\text{lin-out}_i\right) * \left(\sum_j W^2_{ji} \cdot \text{outerr}_j \right)\] \[\frac{\partial W^2_{ij}}{\partial \text{cost}} = \text{lin-hidden}_i\text{outerr}_j\] \[\frac{\partial W^1_{ij}}{\partial \text{cost}} = \text{input}_i \text{hiderr}_j\]Working example (Online picture vis)
Modern approach to ANNs
Introduction to core ideas
Story so far
Modern story
Vanishing gradient problem
ReLU activation function
RMSprop optimization
\(E[g^2] = 0.9 E[g^2]_ {t-1} + 0.1g^2_t\) \(\theta_{t+1} = \theta_t - \frac{\mu}{\sqrt{E[g^2]_ {t}+\epsilon}}\)
LSTMs
Intro to recurrent networks
LSTM architecture, and how it solve VGP
Noise and learning efficiency
Convolutional networks
Overfitting
Standard regularization
Adding term to cost function
\[\text{cost}(y,a) = \text{old-cost}(y,a) + \frac{\lambda}{2n} \sum_{w \in \text{weights}} w^2\]Hardware considerations
Overview of modern deep learning architectures (LSTM, convolution, attention, softmax probabilities)
Solving non-standard problems like adversarial learning (if time)
More resources
http://colah.github.io/
https://en.wikipedia.org/wiki/Activation_function
old
Introductory ideas
Machine learning
Complex natural functions
Hierarchical abstraction
Neural network algorithm
Algebraic construction
Diagram
Input/output format
Weight matrixes - linear functions define abstractions/interactions
Activation function
Backpropagation
Cost function
Applications/examples
###
-
Deep learning and ANNs are not quite the same: deep learning implies backpropogation, ANNs make no mention of that idea.
- More art than science
- So different than other ideas that we don’t have terminology to talk about them (a whole new branch of science)