Accelerating CAS-Offinder
CAS-Offinder is a genomic search tool developed by the Genome Engineering Laboratory at Seoul National University. This tool has a flexible interface and a fast GPU accelerated implementation that makes it quite attractive, both from a biological perspective, as it can be used for many gene technologies, such as TALENs and so it seems to have potential for its users to grow. But of course, this tool could be even more useful and attractive if it was many times faster…
Over the course of this effort, I:
- Improved the core data representation to an efficient bit-packed format (allowing trillions of comparisons per second on a GPU)
- Simplified the algorithm (inner loop is ~20 lines of code, no local memory or hardware specific features used)
- Improved the multigpu support with multithreading (providing linear speedups on large datasets)
- Decreased memory consumption with data pipelining (total memory utilitzation on both CPU and GPU is now consistently under 500MB)
- Added signficiant unit testing for all key logical modules (improving confidence in the accuracy of the implementation)
The final implementation is in my fork of the project here.
The tool
The use case
CAS-Offinder is primarily designed to find off-target sites for CRISPR gene editing technologies. When using this technology, treatment developers choose 1) a protein system and 2) A guide RNA sequence. If the protein and the guide sequence approximately matches the DNA strand in the genome, then the DNA will be cut.
Through its flexible interface, CAS-Offinder can perform searches to find possible cut points for a wide variety of these protein systems.
Genetic search complexities
A genome is a series of nucleotides: A,C,T, or G. So 4 possibilities.
We can see where the string “ATCGC” appears in the genome with a simple string search. The complexity arises with 3 problems
Complexity 1: Symmetric DNA
DNA (unlike RNA) is composed of base-pairs. I.e, it looks like this
3-CAGTA-5
5-GTCAT-3
3 and 5 represent the direction of the nucleotide. However, note that both sides have a 3 end and a 5 end, and so while the system is read from the 5’ end to the 3’ end, it is still symmetrical, i.e. the above sequence and the one below are physically identical
3-TACTG-5
5-ATGAC-3
So we must search both possible representations, as both versions are of equal biological significance.
Complexity 2: Unequal nucleotide treatment
Not all nucleotides are created equally, sometimes two nucleotides are accepted by protein systems with roughly equal probability, while the others are rejected with high probability. To capture this notion of similar treatment, we should be able to specify combinations of nucleotides which are allowed. The interface allows this to be specified easily through mixed-base pairs. So the letter “R” means that it could be A or G. The letter “N” means it could be any nucleotide, which is very useful, as it represents empty space which is ignored by the CRISPR technology.
| A | C | G | T |
|---|---|---|---|
| Adenine | Cytosine | Guanine | Thymine |
| R | Y | S | W | K | M |
|---|---|---|---|---|---|
| A or G | C or T | G or C | A or T | G or T | A or C |
| B | D | H | V | N |
|---|---|---|---|---|
| C or G or T | A or G or T | A or C or T | A or C or G | any base |
Complexity 3: Fuzziness
Genetic systems are highly random, taking place in a complex environment afflicted by kinetic, electrical and even quantum forces by surrounding molecules.
To take into account this final bit of randomness, we should allow some number of mismatches, so that we don’t miss any possible cut sites.
The algorithm
The original cas-offinder tool simply did a search comparing literal charachters. The following is the inner loop:
for (j=0; j<patternlen; j++) {
k = l_comp_index[j];
if ( (l_comp[k] == 'R' && (chr[loci[i]+k] == 'C' || chr[loci[i]+k] == 'T')) ||
(l_comp[k] == 'Y' && (chr[loci[i]+k] == 'A' || chr[loci[i]+k] == 'G')) ||
(l_comp[k] == 'K' && (chr[loci[i]+k] == 'A' || chr[loci[i]+k] == 'C')) ||
(l_comp[k] == 'M' && (chr[loci[i]+k] == 'G' || chr[loci[i]+k] == 'T')) ||
(l_comp[k] == 'W' && (chr[loci[i]+k] == 'C' || chr[loci[i]+k] == 'G')) ||
(l_comp[k] == 'S' && (chr[loci[i]+k] == 'A' || chr[loci[i]+k] == 'T')) ||
(l_comp[k] == 'H' && (chr[loci[i]+k] == 'G')) ||
(l_comp[k] == 'B' && (chr[loci[i]+k] == 'A')) ||
(l_comp[k] == 'V' && (chr[loci[i]+k] == 'T')) ||
(l_comp[k] == 'D' && (chr[loci[i]+k] == 'C')) ||
(l_comp[k] == 'A' && (chr[loci[i]+k] != 'A')) ||
(l_comp[k] == 'G' && (chr[loci[i]+k] != 'G')) ||
(l_comp[k] == 'C' && (chr[loci[i]+k] != 'C')) ||
(l_comp[k] == 'T' && (chr[loci[i]+k] != 'T'))) {
lmm_count++;
if (lmm_count > threshold)
break;
}
}
While the compiler will likely optimize a complex condition like this into something reasonably efficient, and it is honestly a totally reasonable approach, we can do much better by rethinking the data structure.
A bitpacked data structure
Consider the following binary data encoding of a genome
| T | C | A | G |
|---|---|---|---|
| 0001 | 0010 | 0100 | 1000 |
I.e. a bit in a particular location signifies the presence or absence of a nucleotide.
Now, we can encode the mixed base pairs by simply computing the bitwise “or” of the nucleotides. For example
| R | B | N |
|---|---|---|
| 1100 | 1011 | 1111 |
Now, since each nucleotide only takes 4 bits, we can pack 8 nucleotides into a 32 bit word.
ATCGGTAC
=
0100,0001,0010,1000,1000,0001,0100,0010
And we can also pack 8 mixed base pairs into a 32 bit word
CTCGGNRG
=
0010,0001,0010,1000,1000,1111,1100,1000
Now, we can check how many mismatches this part of the genome has by simply computing a bitwise “and” (in C, this is the “&” operator).
0100,0001,0010,1000,1000,0001,0100,0010
&
0100,0001,0010,1000,1000,1111,1100,1000
=
0000,0001,0010,1000,1000,0001,0100,0000
And finally a “popcount” operation which checks the number of set bits.
popcount(0000,0001,0010,1000,1000,0001,0100,0000)
=
6
So we know that 6 off the nucleotides matched, out of a possible 8, so there are 2 mismatches.
To check every possible position in the genome, not just the 8 nucleotide boundaries, some bit-shifting is needed. However, the full inner loop remains quite simple. The following code describes the inner loop.
size_t blocks_avail = 8;
for (size_t k = 0; k < blocks_avail; k++) {
uint32_t mismatches = 0;
for (size_t l = 0; l < blocks_per_pattern; l++) {
uint32_t genome_block = (genome[genome_idx + l] >> (k * 4)) | (genome[genome_idx + l + 1] << ((blocks_avail - k) * 4));
mismatches += popcount(
genome_block & pattern_blocks[pattern_block_idx * blocks_per_pattern + l]);
}
if (mismatches <= max_mismatches) {
// log result
}
}
From a performance standpoint, this has several advantages from the original implementation:
- The memory access pattern is local, regular, and easily cachable
- There are no unpredictable branches anywhere
- Several comparisons happen in parallel in a single instruction
- popcount is hardware accelerated on almost all modern hardware platforms, and is very fast (almost as fast as integer multiplication).
The complete, highly optimized inner loop is still extremely simple:
block_ty shifted_blocks[blocks_per_pattern + 1];
for (size_t i = 0; i < blocks_per_pattern + 1; i++) {
shifted_blocks[i] = genome[genome_idx + i];
}
for (size_t k = 0; k < blocks_avail; k++) {
uint32_t count = 0;
for (size_t l = 0; l < blocks_per_pattern; l++) {
block_ty cur = shifted_blocks[l];
count += popcount(
cur & pattern_blocks[pattern_block_idx * blocks_per_pattern + l]);
}
for (size_t l = 0; l < blocks_per_pattern; l++) {
shifted_blocks[l] =
(shifted_blocks[l] >> 4) |
(shifted_blocks[l + 1] << ((blocks_avail - 1) * 4));
}
shifted_blocks[blocks_per_pattern] >>= 4;
int mismatches = max_matches - count;
if (mismatches <= max_mismatches) {
int next_idx = atomic_inc(entrycount);
match next_item = {
.loc = genome_idx * blocks_avail + k,
.pattern_idx = pattern_block_idx,
.mismatches = mismatches,
};
match_buffer[next_idx] = next_item;
}
}
The reason this is so incredibly efficient is that the blocks_per_pattern is typically small (<=4) and is known at startup time when OpenCL is compiled, so the inner loop can be fully unrolled, and the shifted_blocks array can be replaced by a series of registers. In fact, the pattern_blocks accesses can also be replaced by register access, so the inner loop will likely be left with no memory accesses at all, only register arithmetic.
With this near-optimal hardware setup, we are able to achive truly incredible comparison throughputs:
On a test input file with 91 nucleotides, 50 patterns, and on the human genome with ~3.2 billion base pairs, (and it is symmetric), that is 91*50*3.2*2=29000 billion comparisons.
On this test input, we got the following performance on various hardware platforms:
| Hardware | time | Comparisons (billion/s) |
|---|---|---|
| Dual RTX-2060 GPUs | 5.9545s | 4984 b/s |
| Intel(R) UHD Graphics 620 (on laptop) | 141s | 205 b/s |
| 12-core, 24 thread 1920x Ryzen threadripper CPU | 350.145s | 83.2 b/s |
Note that on this input set, the performance is 10x or greater than the original cas-offinder tool all tested hardware platforms except the popencl CPU platform.
Whole program optimization
The inner loop is not the only performance consideration. We also need to spend as much time in the inner loop as possible, and keep system resources under control.
Performance goals
In order to maximize GPU performance, we should make sure that all GPUs are operating all of the time:
- If possible, file parsing, data preprocessing, postprocessing and file output should not impede core compute procedure.
- Multiple GPUs should execute concurrently and independently to maximize compute efficiency.
In order to keep memory utilization predictable:
- Data that cannot be processed for a long time should not be read from disk.
Pipeline design
To solve all of the above goals, a data pipeline is created. This data pipeline has independent threads for input, output, and each compute device (represented by ovals) and communicate via two buffered channels, one for data input and one for output (represented by boxes).
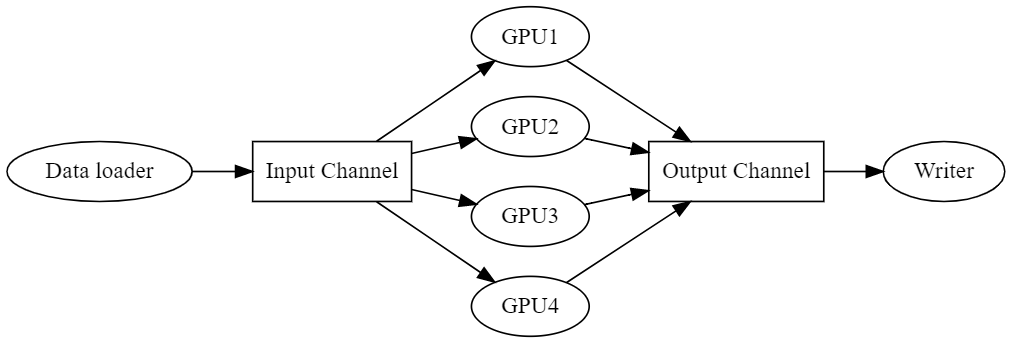
With this simple architecture, all the performance goals are satisfied.
- File processing happens asynchronously, not impeding computation
- Each GPU is controlled via its own thread, operating independently.
- Postprocessing file writing operates asynchronously
- Data is not read if the input channel’s buffer is full, minimizing memory consumption.
Unit testing
Under the test directory are a number of unit tests, orchestrated through a custom (but effective) test framework.
These tests check many edge cases in conversions to and from the 4bit data format, file parsing, searching, and more.
These tests made optimizing certain procedures (file parsing, searching, format conversions) extremely easy and fast—most of the optimizations were implemented in a single day.
Benchmark
Here is a benchmark of the new code vs the original cas-offinder 2.4.1 implementation. Benchmark script here. Hardware was CPU: AMD Threadripper 1920X, GPU: 2x RTX 2060.
| Device | Num Guides | Mismatches | PAM | Guide Length | new code | cas-offinder 2.4.1 |
|---|---|---|---|---|---|---|
| G | 1 | 3 | NRG | 20 | 2.457066535949707 | 7.838363885879517 |
| G | 1 | 3 | NRG | 25 | 2.5289411544799805 | 16.501859664916992 |
| G | 1 | 3 | NNGRRT | 20 | 2.5530526638031006 | 6.3273797035217285 |
| G | 1 | 3 | NNGRRT | 25 | 2.277801036834717 | 6.427332639694214 |
| G | 1 | 3 | TTTN | 20 | 2.2968239784240723 | 14.080754280090332 |
| G | 1 | 3 | TTTN | 25 | 2.269219160079956 | 17.261003017425537 |
| G | 1 | 3 | NNN | 20 | 2.5658657550811768 | 9.768653869628906 |
| G | 1 | 3 | NNN | 25 | 2.4853222370147705 | 27.38359498977661 |
| G | 1 | 6 | NRG | 20 | 2.288862466812134 | 8.168041229248047 |
| G | 1 | 6 | NRG | 25 | 2.296704053878784 | 17.12664294242859 |
| G | 1 | 6 | NNGRRT | 20 | 2.3106417655944824 | 6.413571119308472 |
| G | 1 | 6 | NNGRRT | 25 | 2.2874395847320557 | 6.45048189163208 |
| G | 1 | 6 | TTTN | 20 | 2.597984790802002 | 15.61670446395874 |
| G | 1 | 6 | TTTN | 25 | 2.301694869995117 | 16.070722341537476 |
| G | 1 | 6 | NNN | 20 | 2.313948631286621 | 11.06814956665039 |
| G | 1 | 6 | NNN | 25 | 2.546156406402588 | 32.08479380607605 |
| G | 100 | 3 | NRG | 20 | 3.281158685684204 | 81.62353587150574 |
| G | 100 | 3 | NRG | 25 | 4.345930576324463 | 106.61158084869385 |
| G | 100 | 3 | NNGRRT | 20 | 4.305038928985596 | 14.771099328994751 |
| G | 100 | 3 | NNGRRT | 25 | 4.255571126937866 | 15.478232860565186 |
| G | 100 | 3 | TTTN | 20 | 3.267700433731079 | 41.72032713890076 |
| G | 100 | 3 | TTTN | 25 | 4.387739181518555 | 46.10689091682434 |
| G | 100 | 3 | NNN | 20 | 3.3470168113708496 | 255.67016053199768 |
| G | 100 | 3 | NNN | 25 | 4.296769380569458 | 1038.861836194992 |
| G | 100 | 6 | NRG | 20 | 7.8972320556640625 | 117.8295590877533 |
| G | 100 | 6 | NRG | 25 | 4.395631313323975 | 142.38549041748047 |
| G | 100 | 6 | NNGRRT | 20 | 7.213689565658569 | 18.794063568115234 |
| G | 100 | 6 | NNGRRT | 25 | 4.371814727783203 | 20.25647521018982 |
| G | 100 | 6 | TTTN | 20 | 6.948397159576416 | 53.07967925071716 |
| G | 100 | 6 | TTTN | 25 | 4.3952319622039795 | 56.78704071044922 |
| G | 100 | 6 | NNN | 20 | 20.577077388763428 | 379.30489897727966 |
| G | 100 | 6 | NNN | 25 | 4.327762842178345 | 1509.7268223762512 |
| C | 1 | 3 | NRG | 20 | 3.590397834777832 | 43.46000361442566 |
| C | 1 | 3 | NRG | 25 | 3.6751527786254883 | 43.74400877952576 |
| C | 1 | 3 | NNGRRT | 20 | 3.6508681774139404 | 13.540801286697388 |
| C | 1 | 3 | NNGRRT | 25 | 3.632962703704834 | 12.931318521499634 |
| C | 1 | 3 | TTTN | 20 | 3.759443998336792 | 20.997319221496582 |
| C | 1 | 3 | TTTN | 25 | 3.628269910812378 | 21.615241765975952 |
| C | 1 | 3 | NNN | 20 | 3.641589641571045 | 157.16770362854004 |
| C | 1 | 3 | NNN | 25 | 3.554177761077881 | 157.28540921211243 |
| C | 1 | 6 | NRG | 20 | 3.6152164936065674 | 45.03748655319214 |
| C | 1 | 6 | NRG | 25 | 3.5648601055145264 | 43.65849947929382 |
| C | 1 | 6 | NNGRRT | 20 | 3.6128592491149902 | 13.665508031845093 |
| C | 1 | 6 | NNGRRT | 25 | 3.7108068466186523 | 12.900066137313843 |
| C | 1 | 6 | TTTN | 20 | 3.6672797203063965 | 21.239816188812256 |
| C | 1 | 6 | TTTN | 25 | 3.5897068977355957 | 22.04256582260132 |
| C | 1 | 6 | NNN | 20 | 3.665330648422241 | 164.93094301223755 |
| C | 1 | 6 | NNN | 25 | 3.700547933578491 | 164.99052476882935 |
| C | 100 | 3 | NRG | 20 | 195.8663148880005 | 191.26478362083435 |
| C | 100 | 3 | NRG | 25 | 198.46067905426025 | 201.00600957870483 |
| C | 100 | 3 | NNGRRT | 20 | 197.7969355583191 | 39.44978475570679 |
| C | 100 | 3 | NNGRRT | 25 | 197.9326527118683 | 38.36330270767212 |
| C | 100 | 3 | TTTN | 20 | 197.84042501449585 | 68.67597556114197 |
| C | 100 | 3 | TTTN | 25 | 198.83449029922485 | 73.39102458953857 |
| C | 100 | 3 | NNN | 20 | 199.13335537910461 | 1149.2943522930145 |